What types of questions can you expect on the ACT Math test? Learn how to prep for the concepts and math formulas you’ll face with some ACT math practice.
What To Expect on the ACT Math Test

You will have 60 minutes to answer 60 multiple-choice questions based on “topics covered in typical high school classes.” For those of you who aren’t sure if you went to a typical high school, these questions break down into rather precise areas of knowledge.
The ACT Math Test usually breaks down into 6 questions types: pre-algebra, elementary algebra, and intermediate algebra questions; plane geometry and coordinate geometry questions; and some trigonometry questions.
ACT Algebra
- 14 pre-algebra questions based on math terminology (integers, prime numbers, and so on), basic number theory (rules of zero, order of operations and so on), and manipulation of fractions and decimals
- 10 elementary algebra questions based on inequalities, linear equations, ratios, percentages, and averages
- 9 intermediate algebra questions based on exponents, roots, simultaneous equations, and quadratic equations
Total: 33 questions
ACT Geometry
- 14 plane geometry questions based on angles, lengths, triangles, quadrilaterals, circles, perimeter, area, and volume
- 9 coordinate geometry questions based on slope, distance, midpoint, parallel and perpendicular lines, points of intersection, and graphing
Total: 23 questions
ACT Trigonometry
- 4 questions based on basic sine, cosine, and tangent functions, trig identities, and graphing
Total: 4 questions
ACT Math Formulas
The ACT does not provide any formulas at the beginning of the Math Test. This means you need to memorize relevant formulas, so you can recall them quickly as needed. Don’t panic! Because ACT is so specific about the types of questions it expects you to answer, you can easily prepare to tackle them.
Read More: 6 ACT Math Tips to Improve Your Score
ACT Calculator Policy
Not all standardized tests allow calculators. Fortunately, ACT does. Your calculator can help to save a ton of time on operations that are easy to mess up like multiplying decimals or working with big numbers. The place where you have to be really careful with your calculator, though, is on the easy ones. Be careful with negative numbers!
What kind of calculator should I bring?
TI-89, TI-92, and TI-Nspire CAS model calculators are not allowed on the ACT (among others). In our book ACT Premium Prep, we show you to how solve problems on the TI-83.
If you don’t plan to use a TI-83 on the test, we recommend you make sure your calculator is acceptable for use on the test and that it can do the following:
- handle positive, negative, and fractional exponents
- use parentheses
- graph simple functions
- convert fractions to decimals and vice versa
- change a linear equation into y = mx + b form
ACT Math Practice
You are permitted to use a calculator for these questions. You may use your calculator for any problems you choose, but some of the problems may best be done without using a calculator.
1. What is the largest value of x that solves the equation x 2 - 4x +3 = 0
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
Answer: (C)
This might look like a traditional plug-and-chug problem, but the problem is asking for a specific value, and the answer choices are all real numbers. A great indication that you can plug in the answer. The problem is asking for the largest, so start with choice (E). Does the equation work if x = 5? 5 2 - 4(5) + 3 = 25 - 20 + 3 ≠ 0. Eliminate choice (E). Try choice (D), 4 2 - 4(4) + 3 = 16 - 16 + 3 ≠ 0. Try choice (C), 3 2 - 4 (3) + 3 = 9 - 12 + 3 = 0, It works, and because you're plugging in the answer, you can stop once you've found a correct answer. If you selected choice (A), be careful; this is the smallest value of x that solves the equation.
2. If the area of circle A is 16π then what is the circumference of circle B if its radius is ½ that of circle A ?
(F) 2π (G) 4π (H) 6π (J) 8π (K) 16π
Answer: (G)
If you have one piece of information about a circle, you can find everything else you need. The area of circle A is 16π and because A = π r 2 , the radius of circle A must be 4. If the radius of circle B is half that of circle A , then the radius of circle B must be 2. Then find the circumference of circle B , with C = 2π r = 2π r(2) = 4π , or choice (G).
3. In the word HAWKS, how many ways is it possible to rearrange the letters if none repeat and the letter W must go last?
(A) 5 (B) 15 (C) 24 (D) 120 (E) 650
Answer: (C)
This is problem is asking for arrangements, so start by creating the number of slots you will need:
(1) (2) (3) (4) (5).
There is a restriction on the last slot in that only one letter, W, can go there, so fill this one in first:
(1) (2) (3) (4) (5) 1
Then, fill the rest in as normal, remembering that W is already taken, so there are only four letters left:
(1) 4 (2) 3 (3) 2 (4) 1 (5) 1
Now that you've got the slots filled in, go ahead and multiply the numbers to find the number of possible arrangements:
(1) 4 x (2) 3 x (3) 2 x (4) 1 x (5) 1 = 24 possible arrangements, or choice (C).
4. What is the slope of the line represented by the equation 10 x + 2 x = y + 6 ?
(F) 10 (G) 12 (H) 14 (J) 15 (K) 16
Answer: (G)
In order to find the slope, put this equation into slope-intercept form, or y = mx + b . Combine the x-terms, and subtract 6 from each side to find 12x – 6 = y, in which the m term must be 12, (G).
5. In triangle ABC below, the tan of the marked angle equals
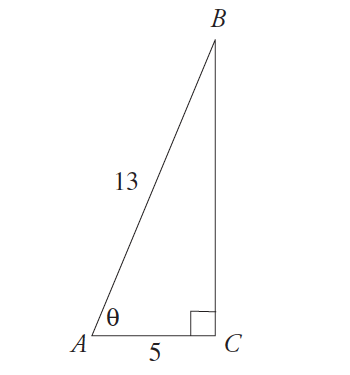
(A) 5 ⁄ 12 (B) 12 ⁄ 13 (C) 17 ⁄ 12 (D) 12 ⁄ 5 (E) 3
Answer: (D)
Use the equation tangent = opposite / adjacent. Your first impulse here may be to solve for the unknown side, but take a close look at where the marked angle is. Its adjacent side is 5, meaning the tangent of that angle must have a denominator of 5. Only (D) has it, so it's the only answer that can work. If you do solve for the unknown side, remember your Pythagorean triples: this is a 5:12:13 triangle, so the unknown side must be 12.
Build the right ACT prep plan for you
Our private tutors will help you build a prep plan that's customized to your score goals, study habits, and schedule.
Read More
Explore Colleges For You
Connect with our featured colleges to find schools that both match your interests and are looking for students like you.
Get Started on Athletic Scholarships & Recruiting!
Join athletes who were discovered, recruited & often received scholarships after connecting with NCSA's 42,000 strong network of coaches.
Best 391 Colleges
170,000 students rate everything from their professors to their campus social scene.



