The MCAT is essentially a science test, but you’ll still need a solid grasp of math fundamentals to score big —and you cannot use a calculator.
Our experts compiled a list of MCAT math topics to prep for along with some tips for doing math calculations by hand.
What math is covered on the MCAT?

The MCAT is primarily a conceptual exam, with little actual mathematical computation. Any math that is on the MCAT is fundamental: just arithmetic, algebra, and trigonometry. There is absolutely no calculus on the MCAT. Math-based problems will appear mostly in the Chemical and Physical Foundations of Biological Systems section . On the other science sections, a basic understanding of statistics as used in research will be helpful.
MCAT Math Tricks
1. Practice for not having a calculator.
You aren’t allowed to use a calculator on the MCAT, so you need to practice doing arithmetic calculations by hand. Fortunately, the amount of calculation you’ll have to do is small. See how you score on our free MCAT practice test .
2. You only have to be reasonably accurate.
Try to make approximations so that you can do the math quickly. On the Chem/Phys section, your MCAT time per question is approximately 1.4 minutes (95 minutes for 67 questions). There simply isn't time for lengthy, complicated math!
Here's how it works. Which of the following calculations for figuring out the value of 23.6 × 72.5 is faster?
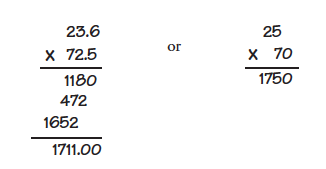
In the one-step calculation on the right, we approximated: 23.6 ≈ 25 and 72.5 ≈ 70. The answer we got in just a few seconds differs from the precise answer by only 2%. For the MCAT, you should always try to approximate so that you can do the math quickly.
3. Remember to pace yourself
If you find yourself writing out convoluted calculations on your scratch paper when you’re working through math-based MCAT problems, it’s important that you recognize that you’re not using your time efficiently. Say to yourself, “I’m wasting valuable time trying to get a precise answer, when I don’t need to be precise.”
4. Include some math review in your MCAT prep
Are you rusty in any of these areas? You'll want to brush up on a few key math concepts during your MCAT prep .
Arithmetic, Algebra, Graphs
- Scientific notation, exponents, and radicals
- Fractions, ratios, and percents
- Equations and inequalities
- x-y plane, lines, and other graphs
Trigonometry
- Pythagorean Theorem
- Sine, cosine, and tangent functions
- Sine and cosine values of common angles
- Inverse functions
- Radian measure
Vectors
- Scalars and vectors
- Addition and subtraction of vectors
- Scalar multiplication
- Vector projections and components
Proportions
- Direct proportions
- Inverse proportions
Logarithms
- Laws of logarithms
Basic Statistics
- Mean, median, mode, range
- Standard deviation, normal distributions
- Percentile
- Variables, sample size, random samples, correlation
- Reliability, validity
- Randomized controlled trial, double-blind experiment
Research Methods
- Graphical analysis and interpretation
- Determining whether results are supported by data presented in figures
- Demonstrating an understanding of basic statistics and research methods
- Interpreting data presented in graphs, figures, and tables
- Drawing conclusions about data and methodology
Get your maximum score with expert MCAT prep
Learn More
Read More
Explore Graduate Programs for You
Explore our featured graduate schools & programs to find those that both match your interests and are looking for students like you.
Best Law Schools
Check out our complete list of 168 law schools, based on surveys of school administrators and over 17,000 students.
Search for Medical Schools
Visit our Med School Hub to explore med schools with our ‘Find Your Med School’ filtered search or visit our Med School Advice pages for info about good MCAT scores or interview question prep.

Find MBA Programs Matched to Your Interests
Explore our featured business schools to find those that are looking for students like you.